The find suggests number theorists need to be a little more careful when exploring the vast. Many mathematicians from ancient times to the present have studied prime numbers. They prefer not to mimic the final digit of the preceding prime, mathematicians have discovered. Web mathematicians are stunned by the discovery that prime numbers are pickier than previously thought. Quasicrystals produce scatter patterns that resemble the distribution of prime numbers.
Web two mathematicians have found a strange pattern in prime numbers — showing that the numbers are not distributed as randomly as theorists often assume. I think the relevant search term is andrica's conjecture. Are there any patterns in the appearance of prime numbers? They prefer not to mimic the final digit of the preceding prime, mathematicians have discovered. Web the results, published in three papers (1, 2, 3) show that this was indeed the case:
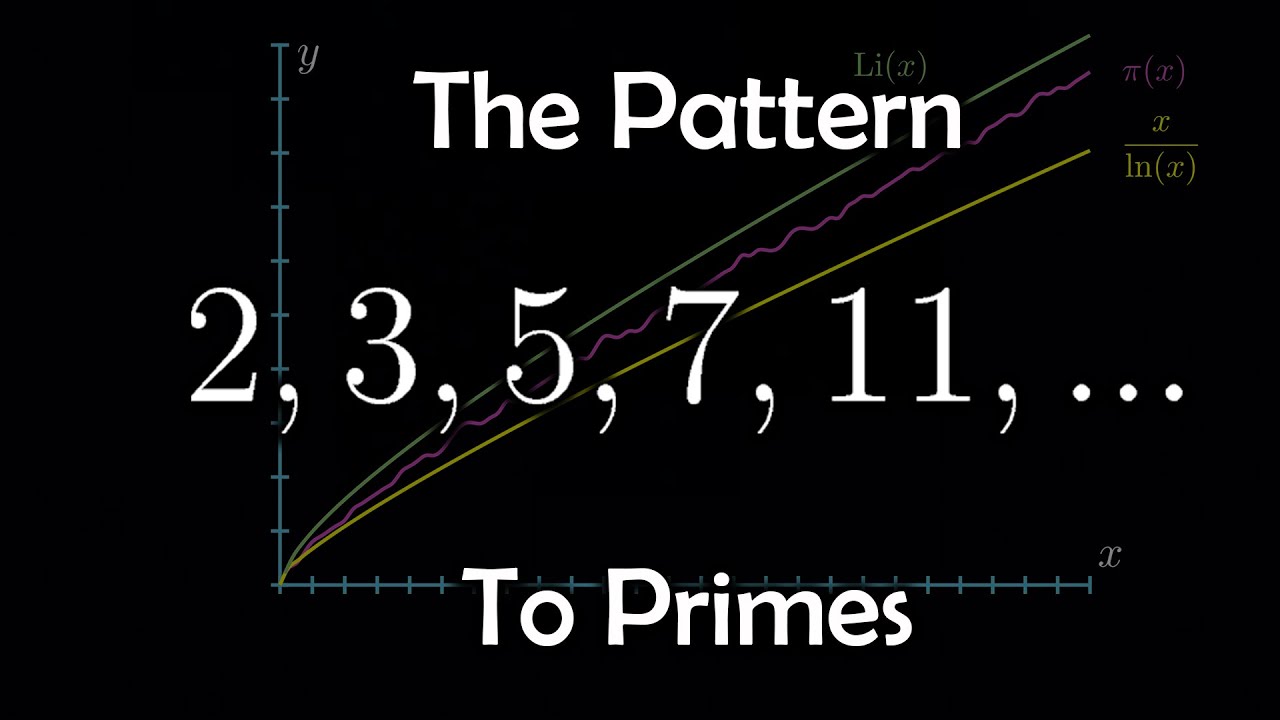
Web the probability that a random number $n$ is prime can be evaluated as $1/ln(n)$ (not as a constant $p$) by the prime counting function. Web now, however, kannan soundararajan and robert lemke oliver of stanford university in the us have discovered that when it comes to the last digit of prime numbers, there is a kind of pattern. This probability becomes $\frac{10}{4}\frac{1}{ln(n)}$ (assuming the classes are random). Web two mathematicians have found a strange pattern in prime numbers—showing that the numbers are not distributed as randomly as theorists often assume. I think the relevant search term is andrica's conjecture.
If we know that the number ends in $1, 3, 7, 9$; The find suggests number theorists need to be a little more careful when exploring the vast. Are there any patterns in the appearance of prime numbers? The other question you ask, whether anyone has done the calculations you have done, i'm sure the answer is yes. Web two mathematicians have found a strange pattern in prime numbers—showing that the numbers are not distributed as randomly as theorists often assume. Quasicrystals produce scatter patterns that resemble the distribution of prime numbers. Web mathematicians are stunned by the discovery that prime numbers are pickier than previously thought. I think the relevant search term is andrica's conjecture. Web two mathematicians have found a strange pattern in prime numbers — showing that the numbers are not distributed as randomly as theorists often assume. Web patterns with prime numbers. Web the results, published in three papers (1, 2, 3) show that this was indeed the case: Web now, however, kannan soundararajan and robert lemke oliver of stanford university in the us have discovered that when it comes to the last digit of prime numbers, there is a kind of pattern. Web the probability that a random number $n$ is prime can be evaluated as $1/ln(n)$ (not as a constant $p$) by the prime counting function. This probability becomes $\frac{10}{4}\frac{1}{ln(n)}$ (assuming the classes are random). Web prime numbers, divisible only by 1 and themselves, hate to repeat themselves.
Web The Probability That A Random Number $N$ Is Prime Can Be Evaluated As $1/Ln(N)$ (Not As A Constant $P$) By The Prime Counting Function.
As a result, many interesting facts about prime numbers have been discovered. I think the relevant search term is andrica's conjecture. The other question you ask, whether anyone has done the calculations you have done, i'm sure the answer is yes. Web two mathematicians have found a strange pattern in prime numbers—showing that the numbers are not distributed as randomly as theorists often assume.
Web Prime Numbers, Divisible Only By 1 And Themselves, Hate To Repeat Themselves.
Web mathematicians are stunned by the discovery that prime numbers are pickier than previously thought. If we know that the number ends in $1, 3, 7, 9$; Are there any patterns in the appearance of prime numbers? Web patterns with prime numbers.
The Find Suggests Number Theorists Need To Be A Little More Careful When Exploring The Vast.
Many mathematicians from ancient times to the present have studied prime numbers. They prefer not to mimic the final digit of the preceding prime, mathematicians have discovered. This probability becomes $\frac{10}{4}\frac{1}{ln(n)}$ (assuming the classes are random). For example, is it possible to describe all prime numbers by a single formula?
Quasicrystals Produce Scatter Patterns That Resemble The Distribution Of Prime Numbers.
Web now, however, kannan soundararajan and robert lemke oliver of stanford university in the us have discovered that when it comes to the last digit of prime numbers, there is a kind of pattern. Web the results, published in three papers (1, 2, 3) show that this was indeed the case: Web two mathematicians have found a strange pattern in prime numbers — showing that the numbers are not distributed as randomly as theorists often assume.

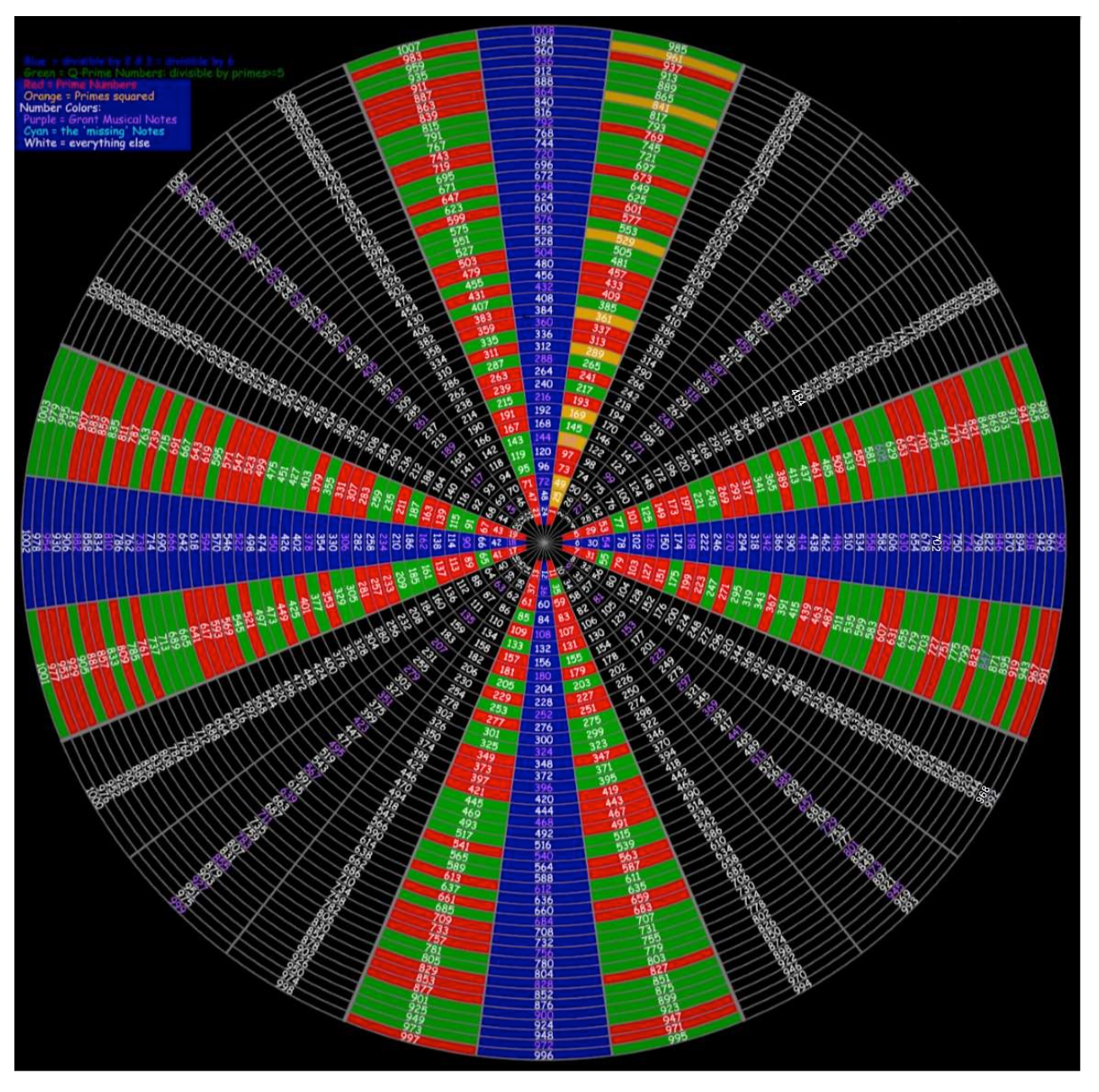
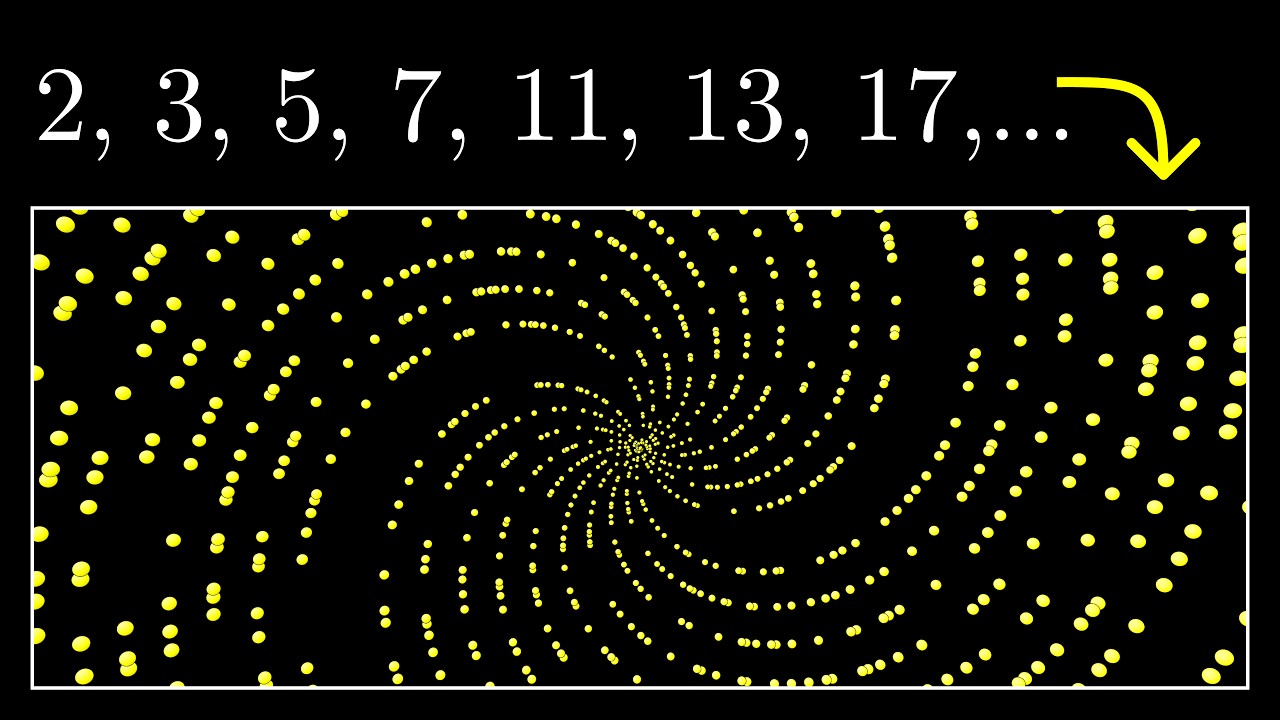
![[Math] Explanation of a regular pattern only occuring for prime numbers](https://i.stack.imgur.com/N9loW.png)